El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
"En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la
suma de los cuadrados de los catetos".
Si un triángulo rectángulo tiene catetos de longitudes 
y 
, y la medida de la hipotenusa es 
, se establece que:
y , y la medida de la hipotenusa es , se establece que:
De la ecuación () se deducen fácilmente 3 corolarios de aplicación práctica:
 |  |  |
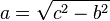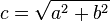* DEMOSTRACIÓN DE TEOREMA DE PITÁGORAS:
Una de las demostraciones geométricas mas conocidas, es la que se muestra a continuación, que suele atribuirse al propio Pitágoras.
A partir de la igualdad de los triángulos rectángulos es evidente la igualdad
a2 + b2 = c2
|  |
- EJERCICIOS:
La hipotenusa de un triángulo rectángulo mide 405.6 m y la proyección de un cateto sobre ella 60 m. Calcular:
No hay comentarios:
Publicar un comentario